
Archytas de Tarento, que nació alrededor del año 435 a. C. en lo que hoy es Taranto, Apulia, Italia, fue otro de una larga lista de brillantes eruditos de la Antigua Grecia, un destacado general militar y estratega que también dejó su huella en los reinos de geometría, física, astronomía y música.
Amigo de Platón, también fue un filósofo brillante. Como científico, perteneció a la escuela pitagórica y se hizo conocido por ser el reputado fundador de la mecánica matemática.
Hijo de Mnesagoras, Archytas fue enseñado por Philolaus, y él mismo fue profesor de matemáticas de Eudoxo de Cnidus. Ambos tenían a Menaechmus como estudiante de matemáticas. Como pitagórico, Arquitas supuestamente creía que solo la aritmética, no la geometría, podía proporcionar una base para demostraciones satisfactorias. Sin embargo, su invención posterior de lo que llegó a llamarse la curva de Archytas refutó esa teoría.
Como se describe en los escritos de Aulus Gellius, cinco siglos después de su vida, tenía fama de haber diseñado y construido el primer dispositivo volador autopropulsado artificial, un modelo con forma de pájaro propulsado por un chorro de lo que probablemente era vapor, que se dice que realmente han volado unos 200 metros.
Conocida hoy como la «Paloma de Archytas», es famosa por ser la base de muchos experimentos en el patio trasero sobre la física del vapor. Su aparato original pudo haber estado suspendido de un alambre o pivote para su vuelo.
Archytas también escribió algunas obras perdidas sobre la ciencia de la mecánica.
Archytas nombró la media armónica, que fue importante mucho más tarde en la geometría proyectiva y la teoría de números, aunque no la inventó. Según Eutocius, Archytas resolvió el problema de doblar el cubo (el llamado problema de Delian) con la construcción geométrica de su curva homónima.
Antes de su época, Hipócrates de Quíos había reducido este problema a encontrar medias proporcionales. La teoría de las proporciones de Arquitas se trata en el libro VIII de los «Elementos» de Euclides, donde la construcción de dos medias proporcionales es equivalente a la extracción de la raíz cúbica.
Según Diogenes Laërtius, esta demostración, que utiliza líneas generadas por figuras en movimiento para construir las dos proporcionales entre magnitudes, fue la primera en la que se estudió la geometría con conceptos de mecánica. La elegante curva de Archytas, que usó en su solución del problema de duplicar el cubo, lleva su nombre.
Brillante estratega fue el Pericles de su tiempo en Magna Grecia
Política y militarmente, Arquitas parece haber sido la figura dominante en Tarento, en lo que entonces era la Gran Grecia, en su generación, algo comparable a Pericles en Atenas medio siglo antes.
Los tarentinos lo eligieron estrategas, o «general», durante siete años seguidos, una medida que les obligó a violar su propio gobierno en contra de sucesivos nombramientos. Al parecer, estaba invicto como general en las campañas de Tarento contra sus vecinos del sur de Italia.
La Séptima Carta de Platón afirma que Arquitas intentó rescatar a Platón durante sus dificultades con Dionisio II de Siracusa.
En su carrera pública, Archytas tenía una reputación tanto de virtud como de eficacia.
Algunos eruditos han argumentado que el erudito Arquitas puede haber servido como modelo para el «rey filósofo» de Platón, y que influyó en la filosofía política de Platón como se muestra en «La República» y otras obras, especialmente como se ve como referencia en su pregunta «¿cómo ¿Una sociedad obtiene buenos gobernantes como Arquitas, en lugar de malos como Dionisio II? ”.
El cráter llamado «Archytas» en la Luna fue nombrado en su honor por la NASA.
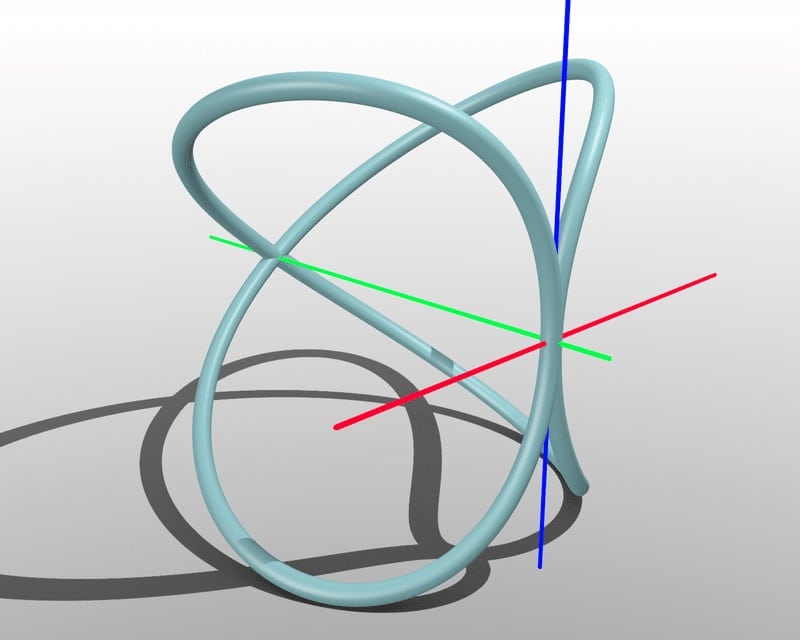
Curva epónima de Archytas
La curva de Arquitas se crea colocando un semicírculo (con un diámetro de d) sobre el diámetro de uno de los dos círculos de un cilindro (que también tiene un diámetro de d) de modo que el plano del semicírculo esté en ángulo recto con el plano del círculo y luego girando el semicírculo alrededor de uno de sus extremos en el plano del diámetro del cilindro. Esta rotación cortará una parte del cilindro que forma la curva de Archytas.
Otra forma de pensar en esta forma es que la curva de Archytas es básicamente el resultado de cortar un toro (una superficie o sólido) formado al girar una semiesfera de diámetro d fuera de un cilindro también de diámetro d. Un cono puede pasar por los mismos procedimientos que también producen la curva de Archytas. Archytas usó su curva para determinar la construcción de un cubo con un volumen de un tercio del de un cubo dado.
Aunque amigo de Platón, tras su invención de la curva, fue criticado por “contaminar” la pureza de la geometría con la mecánica.
Plutarco dice en sus «Simposiacos», Libro VIII, Pregunta 2: «Y, por lo tanto, al mismo Platón no le agradan Eudoxo, Arquitas y Menaecmo por esforzarse en reducir la duplicación del cubo a operaciones mecánicas; porque así todo lo bueno de la geometría se perdería y corrompería, volviendo a las cosas sensibles, y no elevándose hacia arriba y considerando imágenes inmateriales e inmortales, en las que Dios, versado, es siempre Dios ”.
En música, la mayor contribución de Archytas fue la creación de proporciones que presentan un sistema interválico interrelacionado. Las proporciones de Arquitas fueron providencialmente preservadas por Ptolomeo.
Dado que gran parte de la teoría musical griega antigua se ha perdido este sistema; que se registró en la «República» de Platón, ofrece pruebas valiosas sobre la música griega prearistoxeniana; especialmente sobre la armonía y la técnica de transposición, que más tarde se desarrollaron en sistemas completos de octava. especies y tonoi.
Vea las últimas noticias de Grecia y el mundo en Greekreporter.com . Comuníquese con nuestra sala de redacción para informar una actualización o enviar su historia, fotos y videos. Siga a GR en Google News y suscríbase aquí a nuestro correo electrónico diario.







